ANIMATIONS USING TILING

In-place animation consists of considering the tile as the frame of a graphic object that changes over time. The succession of these frames, at the right speed, will give the illusion of an animation.

The modification of the tile can be done at runtime (real time “in place” animation) or by precalculating the tiles that make up the animation (precalculated “in place” animation).

The advantage of the first approach is that it does not occupy spaces in the special area; however, updating the frame will require computing power and it cannot be too complex.

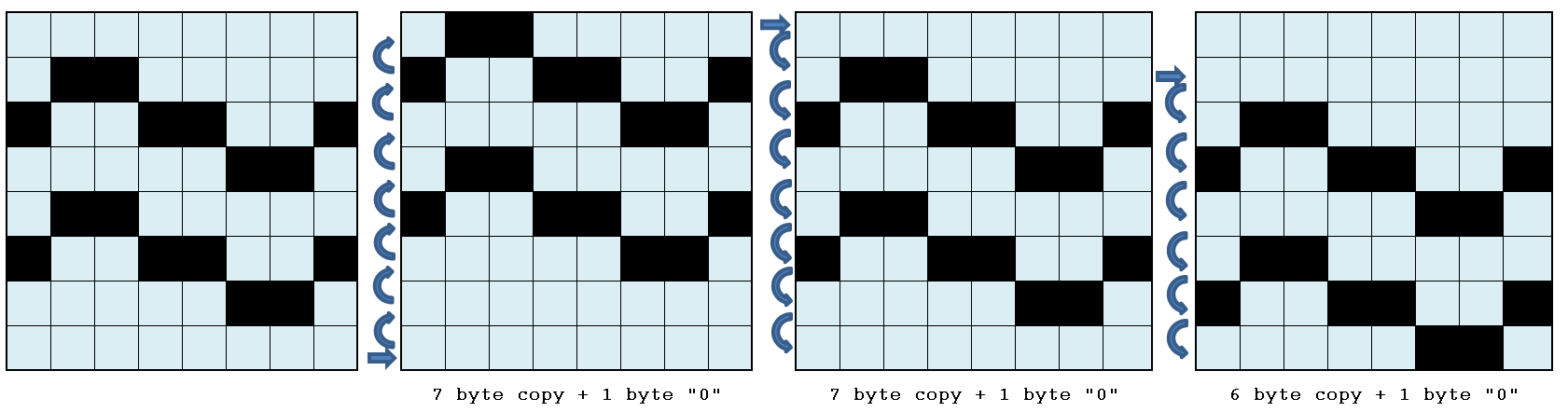
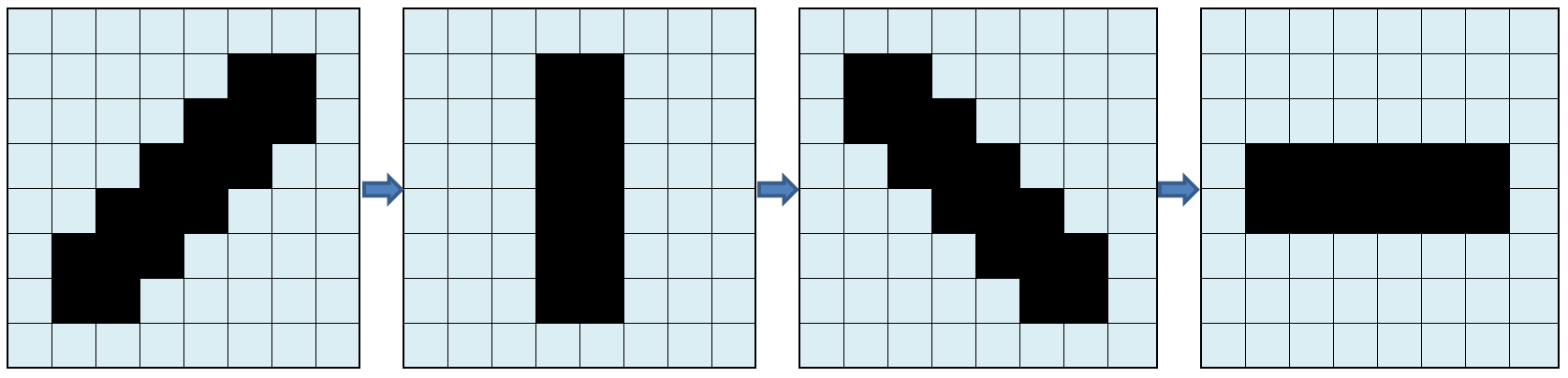
An example of this approach is a 1-pixel vertical wave slide, to simulate a wave. Given a tile of 8×8 pixes, the scrolling of a pixel is an operation that requires 6 or 7 copy operation and 1 byte clearing.

The advantage of the second approach is speed and that there are no limits to the complexity of the operation; on the other hand, it requires the prior allocation of all the frames, which takes away space from the special area.

An example of this approach is the spinning of a wheel, drawn freehand, on its axis, which requires no less than 8 frames and which cannot be done in real time due to the nature of the mathematical operations underlying a rotation.

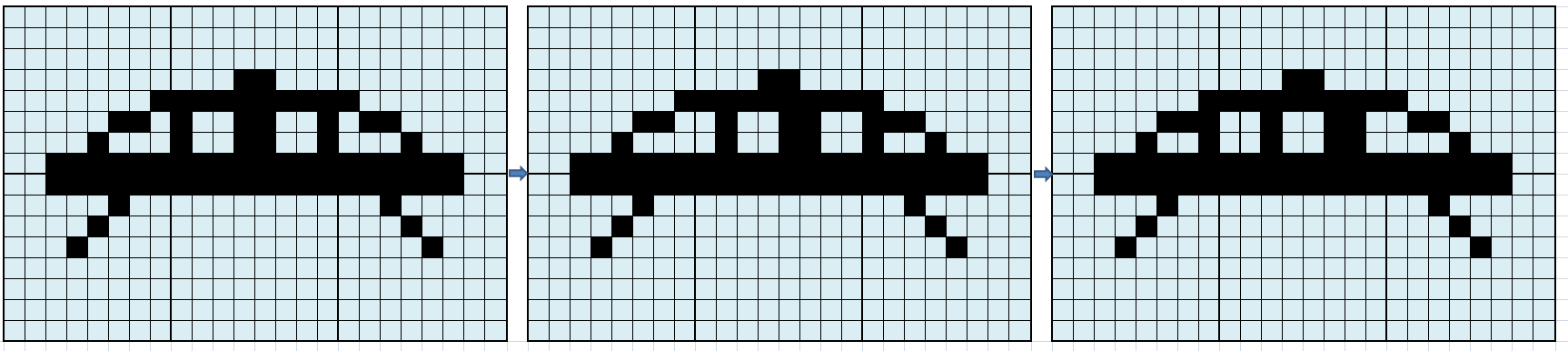
If the object to be animated is composed of several tiles, that is, it is a real tile set, the real-time calculation approach is even less feasible, due to the increase in the computational costs of the update. In such cases it is preferred to draw the frames that make up the animation, transform them into tiles and consider each tile that makes up the graphic object as an independent animation:

By having the appropriate software, it will also be possible to save space by detecting any identities between tiles in different positions, which will allow optimization in the number of required tiles.

The movement of a tile can take place in two ways: discreetly or fluidly. The difference between the two modes is that the discrete movement is “jerky” because the tile is moved to the immediately adjacent box (horizontally or vertically) while the fluid movement guarantees a single pixel movement in the same direction.

The discrete mode does not need any particular explanation, given that it is the simplest implementation or rather the movement of only the index relative to the arrival tile, leaving the original one empty. This type of movement makes that the graphic object coincide with the tile.

The fluid mode, on the other hand, is more complex to implement because the video hardware does not provide any primitive to perform this type of movement. To emulate it, two tiles will have to be redrawn: the one of origin of the displacement and the one of arrival of the displacement. This implies that there is no longer a direct correspondence between the graphic object and the tile, since two tiles participate in drawing it.

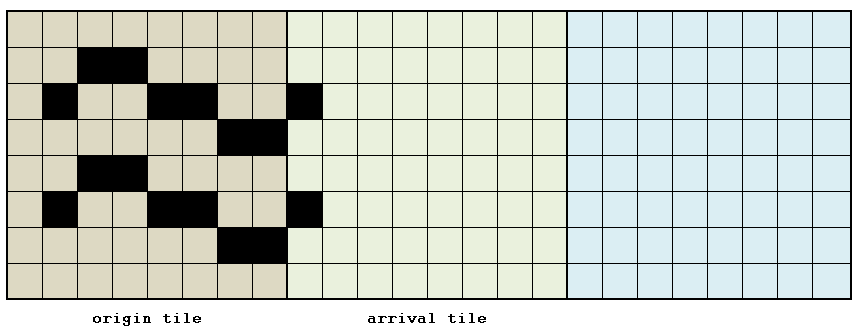
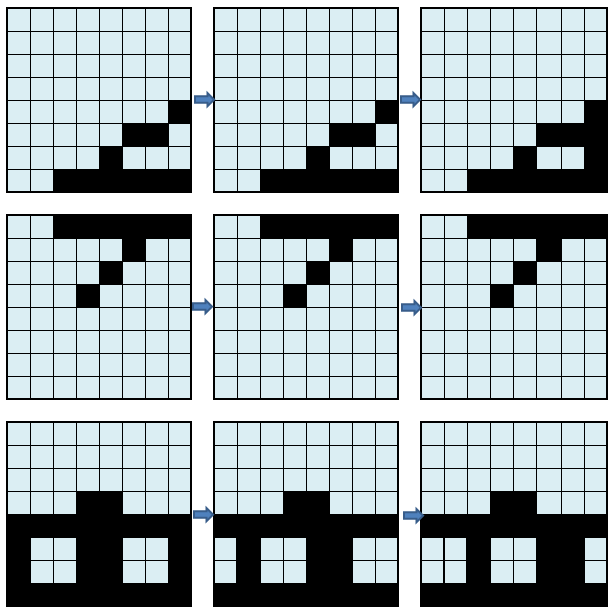
The redraw consists in shifting (to the right or down) of a pixel from the tile that represents the graphic object, and in bringing this pixel back to the arrival tile. By repeating these operations cyclically until the width / height of a tile is complete, we obtain a movement equal to the width / height of a tile. By repeating the whole process several times, we get the displacement of the graphic object by arbitrary distances.

Although shifting are simple operations, the central processor in retrocomputers is usually too slow to be able to perform this type of operation in real time on a large number of tiles: it would result in the inability to perform movements of many tiles.

To ensure acceptable performance, it is therefore necessary to pre-calculate all the intermediate tiles of the movement, treating them as “derived” tiles of the original one:

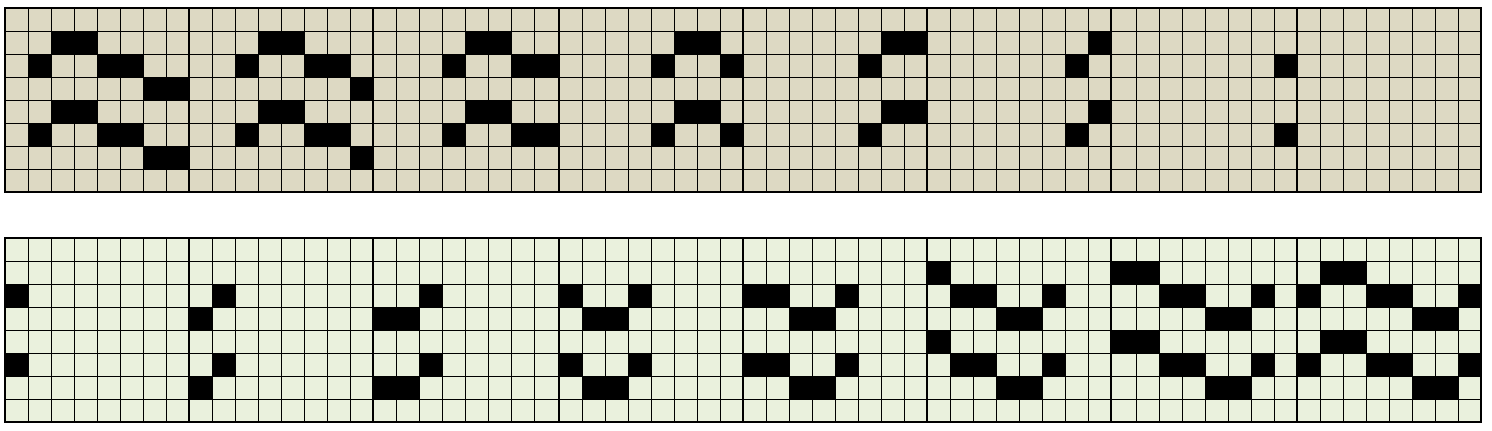
In the simplest case, in which you want to slide a graphic object of the size of a tile, if the tile is formed by a matrix of RxC pixels, the horizontal movement will require 2xR intermediate tiles (R for “exit” and R for “entry” ) while the vertical one will require 2xC (C of “exit” and C of “entry”).

Once the intermediate tiles have been calculated, the algorithm for rendering the displacement must select, within these precalculated tiles, the two that represent the optimal configuration for the instantaneous position of the displacement, by copying their indexes to the expected positions. These operations are certainly faster.

In this case, it must be taken into account that what you want to move is not a single tile but a tile set.

If the tile is formed by a matrix of RxC pixels and the tileset by a set of 2×3 tiles, the horizontal shift will require 2x2xR intermediate tiles (R of “exit” and R of “entry” between the first and second tile, as many between the second and third) while the vertical one will require 3x2xC (C of “exit” and C of “entry” for each pair of tiles).